ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΣΑΦΟΥΣ ΛΟΓΙΚΗΣ

Για να εισαχθούμε στην αντίληψη του ασαφούς συνόλου, ας θυμηθούμε την δύ-τιμη λογική, η οποία απετέλεσε τον ακρογωνιαίο λίθο οποιοδήποτε μαθηματικού μοντέλου χρησιμοποιήθηκε. Μια θεμελιώδη αρχή που ανέτειλε από αυτή την λογική είναι το ότι επέβαλλε μια διχοτόμηση οποιοδήποτε μαθηματικού μοντέλου ενός δεδομένου θέματος. Με άλλα λόγια, παίρνοντας ένα αντικείμενο, άσχετα με την πολυπλοκότητα που έχει, το αναγκάζουμε να ταυτιστεί με μία από τις προκαθορισμένες κατηγορίες την αυστηρή (rigid) ή την συμπληρωματική της (για παράδειγμα καλό-κακό, κανονικό-ανώμαλο, μονό-ζυγό, άσπρο-μαύρο κλπ.)
Μερικές φορές αυτή η κατάταξη έχει έννοια, σε άλλες όμως περιπτώσεις παρουσιάζει μερικά σοβαρά και εμφανή διλήμματα. Για παράδειγμα, στην μελέτη των ακεραίων αριθμών, δύο κατηγορίες όπως οι μονοί και οι άρτιοι αριθμοί μπορούν να οριστούν χωρίς κανέναν δισταγμό, και οποιοσδήποτε ακέραιος αριθμός μπορεί με αυτόν τον τρόπο να ταξινομηθεί μέσα σ΄ αυτό το πλαίσιο χωρίς δυσκολία.
Παρ΄ όλα αυτά, σε πολλές ηλεκτρομηχανολογικές εργασίες, αντιμετωπίζουμε ταξινομήσεις που δεν ορίζονται σαφώς (ill-defined) και δεν κατέχουν καθαρά και γερά θεμελιωμένα σύνορα. Ας υποθέσουμε, για παράδειγμα, μερικές τέτοιες κατηγορίες όπως ψηλός άνθρωπος, μεγάλη ταχύτητα, σημαντικό λάθος, μέση πίεση κλπ. Όλα αυτά μεταφέρουν μια χρήσιμη πληροφορία η οποία είναι προφανής στην καθιερωμένη επικοινωνία. Ωστόσο η διαχωριστική γραμμή μεταξύ δεκτού και απόρριψης ενός δεδομένου αντικειμένου για μια τέτοια τάξη δεν έχει τεκμήρια. Εδώ, γίνεται φανερό ότι η δυνατότητα να αξιοποιήσουμε την δυαδική λογική για να περιγράψουμε αυτές τις τάξεις, δεν εφαρμόζεται ικανοποιητικά.
Ένα ιστορικό παράδειγμα που δείχνει το πώς διάφορα μοντέλα που βασίζονται στην δύ-τιμη λογική μπορούν να αναπτύξουν ανεπιθύμητα φαινόμενα μπορούμε να αντλήσουμε από την αρχαία Ελληνική σοφιστεία. Το παράδειγμα του σωρού των κόκκων λέει,
" ... ένας κόκκος δεν κάνει έναν σωρό, δύο κόκκοι δεν κάνουν ένα σωρό ούτε τρεις ... από την άλλη μεριά ο καθένας θα συμφωνήσει ότι 100 εκατομμύρια κόκκοι δημιουργούν έναν σωρό. Ποίο όμως είναι το αποδεκτό μέγεθος; Μπορούμε να πούμε ότι 325 ή 647 κόκκοι δεν κατασκευάζουν έναν σωρό αλλά τον κατασκευάζουν 325648 κόκκοι; "
Με μια ματιά, είναι προφανές ότι μια απάντηση του τύπου "ναι-όχι" δεν μπορεί να είναι ικανοποιητική απάντηση σ΄ ένα τέτοιο πρόβλημα. Τελικά, κάθε όριο x0 που χρησιμοποιείται στον ορισμό της ιδιότητας του σωρός(x):
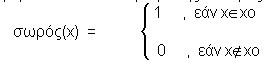
μπορεί να συνεισφέρει σε ένα πολύ απλοποιημένο και ακατόρθωτο μοντέλο αυτού του όρου. Η εννοιολογική αδυναμία αυτού του Δυαδικού μοντέλου είναι άκαρπη όταν επιχειρείται να βρεθεί με ακρίβεια η τιμή του ορίου.
Το κλειδί της έκδοσης των ασαφών συνόλων είναι το ότι κάποιος μπορεί να επεκτείνει σημαντικά την σημασία του συνόλου δεχόμενος διαφορετικούς βαθμούς κτησιμότητας, που αναφέρονται και σαν τιμές μελών. Αυτό ανακουφίζει το προηγούμενο πρόβλημα, συμπεριλαμβάνοντας όλες τις ενδιάμεσες καταστάσεις μεταξύ του καθολικού (ολοκληρωτικού) συνόλου μελών και του συνόλου των μη μελών. Σε αντίθεση, όπως αναφέρθηκε προηγουμένως, με την θεωρία συνόλων που κάποιος είναι περιορισμένος στα όρια των δύο αριθμών 0 και 1.
Επίσης, ακόμα και στα μαθηματικά, μπορούμε να αντιμετωπίσουμε μερικές λογικές με βαθμιαία παρά με απότομα σύνορα. Ένα τέτοιο παράδειγμα είναι: ο διεσπαρμένος (sparse) πίνακας, μία κατά προσέγγιση γραμμική συνάρτηση σε μια μικρή περιοχή του x0 ή ένας αρρωστημένος(ill-conditioned) πίνακας. Εδώ δεχόμαστε αυτές τις λογικές μιας και μεταφέρουν χρήσιμες πληροφορίες σχετικά με το πρόβλημα που μελετάμε. Προφανώς, δεν αντιμετωπίζονται σαν ουσιαστικά ελαττώματα στην καθημερινή μας γλώσσα αλλά μάλλον σαν μελλοντικό πλεονέκτημα, δείχνοντας την ικανότητα μας να γενικεύουμε και να αντιλαμβανόμαστε την γνώση.
Μολαταύτα, μπορούμε να πούμε ότι αυτές οι λογικές εξαρτώνται έντονα από τα περιεχόμενα τους και οι ορισμοί τους δεν είναι με κανένα τρόπο παγκόσμιοι. Για παράδειγμα, η έννοια του "αρρωστημένου πίνακα" μπορεί να εξαρτηθεί άμεσα από τον τύπο του υπολογιστή που χρησιμοποιεί κάποιος στην εφαρμογή που έχει υπ" όψιν του.
Από την παραπάνω γενική συζήτηση πηγάζει η αναγκαιότητα για ένα βολικό, ευλύγιστο και εύκολα κατανοήσιμο εργαλείο που να χειρίζεται την ασάφεια. Έτσι λοιπόν η βασική ιδέα των ασαφών συνόλων αποτελεί μια ελκυστική λύση για να ακολουθήσει κανείς.
Όπως αναφέρθηκε, τα ασαφή σύνολα αλλάζουν τους βασικούς όρους ενός συνόλου για να επιτρέψουν ομαδοποίηση ενδιάμεσων βαθμών. Όσο υψηλότερη είναι η τιμή μιας ομάδας ενός συγκεκριμένου αντικειμένου x με την λογική (ασαφούς συνόλου) Α, ας πούμε Α(x), τόσο δυνατότερος είναι ο δεσμός του x με την κατηγόρια που περιγράφεται από το Α.
Για παράδειγμα, ορίζοντας μια ασαφή λογική όπως ένα μεγάλο θετικό λάθος σταθερής κατάστασης που εκφράζεται επί %, μπορούμε να πούμε ότι 70% του λάθους σταθερής κατάστασης γεμίζει την κατηγορία σε ένα βαθμό ίσο με 0.87, ενώ η στάθμη του 0.01 % χαρακτηρίζεται από τον βαθμό της ομάδας που ισούται με μηδέν.

Δείτε επίσης