ΑΝΑΣΚΟΠΗΣΗ ΑΣΑΦΟΥΣ ΕΛΕΓΚΤΗ

Πριν προχωρήσουμε σε μια αναλυτική περιγραφή του ασαφούς ελεγκτή, είναι αναγκαίο να αποκτήσουμε μια καθαρή εικόνα για τον τρόπο με τον οποίο ο ανθρώπινος εγκέφαλος λειτουργεί για να δώσει λύσεις σε καθημερινά προβλήματα. Για παράδειγμα, το παρκάρισμα του αυτοκινήτου, η τακτοποίηση των ρούχων μας σε ένα σάκο, η τοποθέτηση ενός εύθραστου αντικειμένου, η αναγνώριση προσώπων, είναι μερικά προβλήματα με τα οποία ερχόμαστε αντιμέτωποι καθημερινά. Σε γενικές γραμμές ο τρόπος αντιμετώπισής τους είναι κοινός: αρχικά συγκεντρώνουμε όλες τις απαραίτητες πληροφορίες και με τη βοήθεια της εμπειρίας μας παίρνουμε μια σειρά από πρωτοβουλίες. Στη συνέχεια, παρακολουθώντας τα αποτελέσματα των ενεργειών μας μπορούμε αν είναι απαραίτητο να τις μεταβάλλουμε, προκειμένου να πετύχουμε το επιθυμητό αποτέλεσμα.
Αν λοιπόν επρόκειτο να αντικατασταθεί ο ανθρώπινος παράγοντας σε μια διαδικασία ελέγχου, το σύστημα που θα χρησιμοποιούνταν θα έπρεπε να συμπεριφέρεται σύμφωνα με τα παραπάνω. Ένα τέτοιο σύστημα ονομάζεται έμπειρο, ονομασία που προέρχεται από το γεγονός ότι με κάποιο τρόπο έχει αποθηκευμένη μέσα του μια ποσότητα γνώσης στην οποία βασίζεται για να παίρνει αποφάσεις. Η όλη διαδικασία ελέγχου προϋποθέτει σχεδόν πάντα την ύπαρξη ενός κλειστού συστήματος, πράγμα που σημαίνει ότι ο ελεγκτής παρακολουθεί τα αποτελέσματα των ενεργειών του (αυτό που ονομάζουμε ανάδραση). Δύο είναι οι απαραίτητες προϋποθέσεις για τη σχεδίαση ενός τέτοιου κλειστού συστήματος:
1) Το σύστημα το οποίο πρόκειται να ελεγχθεί πρέπει να είναι γνωστό. Αυτό σημαίνει ότι ο σχεδιαστής πρέπει να γνωρίζει πως θα συμπεριφερθεί το σύστημα σε μια δεδομένη είσοδο. Η γνώση αυτή θα αποτελέσει και την "εμπειρία" του συστήματος.
2) Το αποτέλεσμα του ελέγχου πρέπει να καθοριστεί με μαθηματικό τρόπο χρησιμοποιώντας τις μεταβλητές του συστήματος. Στο αποτέλεσμα αυτό θα αναφέρεται ο ελεγκτής για να παρακολουθεί την πορεία των ενεργειών του.
Σύμφωνα με τις δύο παραπάνω προϋποθέσεις, ο σχεδιαστής μπορεί να κατασκευάσει ένα μοντέλο για το σύστημα που πρόκειται να ελέγχει, και να δοκιμάσει τον ελεγκτή του σε αυτό το μοντέλο. Με αυτό τον τρόπο σχεδιάζονται όλοι οι κλασσικοί αναλογικοί ελεγκτές.
Στην πράξη όμως, όταν η πολυπλοκότητα του συστήματος αυξάνει, και οι δύο παραπάνω προϋποθέσεις σπάνια ικανοποιούνται. Για την μεν πρώτη, επειδή είναι πολύ δύσκολο να κατασκευάσουμε ένα μοντέλο που να λαμβάνει υπ` όψιν του όλες τις παραμέτρους του συστήματος και για τη δεύτερη επειδή είναι πρακτικά αδύνατο να παρακολουθούμε την ακριβή κατάσταση του συστήματος. Έτσι, παρατηρούμε συχνά αυτό που αποκαλείται "υπέρ-μοντελοποίηση". Μπορεί δηλαδή για ένα σχετικά απλό πρόβλημα να κατασκευαστούν τεράστιες και πολύπλοκες εξισώσεις. Αυτή όμως η προσέγγιση σίγουρα δεν αποτελεί λύση.
Στην καθημερινή μας ζωή όμως βλέπουμε συχνά ανθρώπους να κάνουν συχνά σχεδόν τέλεια τη δουλειά τους χωρίς όμως να μπορούν να δώσουν λεπτομερής εξηγήσεις για τις συγκεκριμένες ενέργειές τους. Εδώ φυσικά βρίσκεται κρυμμένη η εμπειρία. Αυτή την εμπειρία αν δώσουμε στον ελεγκτή μας τότε σίγουρα θα έχουμε ένα πολύ καλό αποτέλεσμα.
Το ερώτημα που προκύπτει αμέσως είναι πως θα μεταδώσουμε αυτή τη γνώση (εμπειρία) στο σύστημά μας. Η απάντηση εδώ βρίσκεται στη γενικευμένη έννοια της πρότασης. Με τον όρο πρόταση θεωρούμε μια σχέση μεταξύ κάποιων μεταβλητών. Μια πρόταση περιέχει γνώση που δεν είναι τίποτε άλλο από το νόημά της. Έτσι, η μαθηματική αναπαράσταση της πρότασης αυτομάτως δίνει ένα τρόπο αναπαράστασης της γνώσης. Όμως όλες οι προτάσεις δεν έχουν πάντα μαθηματικά πλήρως καθορισμένο νόημα. Εδώ βέβαια εισάγονται με φυσιολογικό τρόπο οι αρχές της ασαφούς λογικής. Τα προτερήματα μιας τέτοιας προσέγγισης είναι ότι:
1. Δεν χρειάζεται ένα πλήρως καθορισμένο μοντέλο για το σύστημα που πρόκειται να ελεγχθεί.
2. Δεν είναι απαραίτητο να έχουμε πλήρεις πληροφορίες για την κατάσταση του συστήματος που ελέγχουμε.
Ο αναγνώστης εδώ μπορεί εύκολα να συμπεράνει ότι οι απαραίτητες προϋποθέσεις για τη σχεδίαση ενός συστήματος με τον κλασσικό τρόπο δεν χρειάζεται να εκπληρώνονται τώρα.
Όλη η ευελιξία ενός ασαφούς ελεγκτή βρίσκεται στο γενικά αποδεκτό πρότυπο των κανόνων που χρησιμοποιεί. Για παράδειγμα, αν το σύστημα που ελέγχουμε απέχει πολύ από την επιθυμητή κατάσταση, τότε σχεδόν πάντα πρέπει να λάβουμε μια σημαντική ενέργεια για να το επαναφέρουμε. Αυτός είναι ένας κανόνας που σε όλα τα συστήματα είναι εφαρμόσιμος. Τι σημαίνει όμως "απέχει πολύ" και "σημαντική ενέργεια"; Το παράδειγμα αυτό δείχνει την ασάφεια που εισάγει η γενικότητα και την αναγκαιότητα της ασαφούς λογικής.
Στα παρακάτω θα θεωρούμε για απλότητα, ότι το σύστημα που θέλουμε να ελέγχουμε είναι μίας εισόδου και μίας εξόδου. Δηλαδή, κάθε στιγμή το σύστημα μας δίνει μία έξοδο που χαρακτηρίζει την κατάσταση του συστήματος και δέχεται μία είσοδο σύμφωνα με την οποία μεταβάλλει την κατάστασή του. Επιπλέον πάντα είναι γνωστή η επιθυμητή κατάσταση του συστήματος. Έτσι μπορούμε να υπολογίζουμε το λάθος Ε και τη μεταβολή του λάθους ΔΕ σε κάθε χρονική στιγμή. Ο ελεγκτής δίνει προς το ελεγχόμενο σύστημα μια έξοδο U. Μπορούμε τώρα με αυτές τις παραδοχές να περιγράψουμε το γενικευμένο μοντέλο της δομής του ασαφούς ελεγκτή. Τα βασικά τμήματα από τα οποία αποτελείται είναι:
1. Ένα σύνολο από κανόνες ελέγχου που αποτελούν και τη γνώση του ελεγκτή. Οι κανόνες αυτοί περιγράφονται με συμβολικό τρόπο. Η μορφή αυτού του συνόλου δίνεται:
αν Ε1 και ΔΕ1 τότε U1
αλλιώς
αν Ε2 και ΔΕ2 τότε U2
αλλιώς
.
.
.
αν Εn και ΔΕn τότε Un
Η σημασία των παραπάνω κανόνων είναι ότι αν το λάθος είναι Εi και η μεταβολή του λάθους ΔΕi τότε πρέπει να λάβουμε την ενέργεια Ui. Προφανώς υπάρχει ένα πεπερασμένο πλήθος κανόνων που θα δούμε στη συνέχεια πως καλύπτουν όλες τις περιπτώσεις. Το βασικό χαρακτηριστικό εδώ είναι η υλοποίηση των εκφράσεων για όλες τις μεταβλητές. Τόσο το λάθος όσο και η μεταβολή του λάθους και η ενέργεια ελέγχου είναι ασαφή σύνολα. Δηλαδή στους κανόνες ελέγχου οι μεταβλητές δεν προσδιορίζονται ακριβώς. Έτσι, ένας κανόνας ελέγχου μπορεί να είναι: "Αν το λάθος είναι θετικό μικρό και η μεταβολή του λάθους είναι σχεδόν μηδέν τότε η ενέργεια ελέγχου είναι αρνητική μικρή". Το μόνο που μένει να κάνουμε εδώ είναι να προσδιορίσουμε με ασαφή σύνολα τις ποσότητες "θετικό μικρό", "σχεδόν μηδέν" και "αρνητικό μικρό". Στο παρακάτω σχήμα βλέπουμε μια πιθανή υλοποίηση:
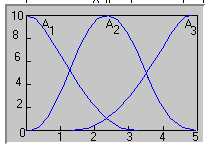
Συνήθως οι κανόνες ελέγχου δίνονται με ένα πίνακα της μορφής:
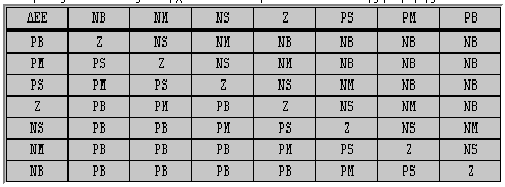
όπου:
PB θετικό μεγάλο
PM θετικό μεσαίο
PS θετικό μικρό
Z μηδέν
NS αρνητικό μικρό
NM αρνητικό μεσαίο
NB αρνητικό μεγάλο
Στον παραπάνω πίνακα όλοι οι κανόνες ελέγχου δίνονται από την οριζόντια και την κάθετη θέση του πίνακα μαζί με το περιεχόμενο της κάθε θέσης. Είναι φυσικά πιθανό κάποιες θέσεις του πίνακα να είναι κενές πράγμα που σημαίνει ότι ο αντίστοιχος κανόνας δεν συμπεριλαμβάνεται. Η αναπαράσταση τώρα των κανόνων με μαθηματικά έχει ως εξής:
Κάθε κανόνας αποτελεί μια ασαφή σχέση Ri=ΕixΔΕixUi και το σύνολο των κανόνων είναι η τομή αυτών των σχέσεων R=R1+R2+...+Rn. Για παράδειγμα, με min-max σύνθεση, η τιμή της σχέσης για μια τριάδα ε,δε,u δίνεται:
R(ε,δε,u)=max1£i£nmin{Εi(ε),ΔΕi(δε),Ui(u)}
2. Ο μηχανισμός συνεπαγωγής. Εδώ γίνονται οι απαραίτητοι υπολογισμοί με βάση την είσοδο του ελεγκτή για τον υπολογισμό της εξόδου. Η είσοδος του ελεγκτή δίνεται από δύο ασαφή σύνολα Ε και ΔΕ. Τότε, το αποτέλεσμα του μηχανισμού συνεπαγωγής είναι η παραγωγή ενός ασαφούς συνόλου U που περιέχει την ενέργεια ελέγχου. Έτσι:
U=(ExΔΕ)nR
ή
U(u)=maxε,δε min{Ε(ε),ΔΕ(δε),R(ε,δε,u)}
Θα δείξουμε στη συνέχεια ένα πολύ βασικό αποτέλεσμα που δείχνει και τη λογική που κρύβεται στον τρόπο παραγωγής του συνόλου ελέγχου. Ισχύει:
U=Θi=1..n(Λi*Ui)
όπου Λi είναι ένα σύνολο με σταθερή συνάρτηση ομάδας (στη συνέχεια θα το συναντήσουμε και σαν σταθερά που θα τη συμβολίζουμε λi) που δίνεται από τη σχέση:
Λi=min{Π(E|Ei),Π(ΔΕ|ΔΕi)}
όπου Π είναι το μέτρο πιθανότητας το οποίο δίνει ένα μέτρο της επικάλυψης των δύο ορισμάτων του. Η απόδειξη της παραπάνω σχέσης προκύπτει πολύ εύκολα αν αναπτύξουμε τη σχέση που δίνει τη συνάρτηση ελέγχου. Φαίνεται όμως πολύ καθαρά τώρα η σημασία της παραπάνω σύνθεσης. Για κάθε είσοδο που έρχεται στον ελεγκτή, δοκιμάζεται κατά πόσο αυτή ταιριάζει με κάθε κανόνα ελέγχου. Έτσι παράγεται ένας αριθμός για κάθε κανόνα που δείχνει το επίπεδο ενεργοποίησής του. Για παράδειγμα, θα μπορούσαμε να έχουμε την παρακάτω κατάσταση:
Ο κανόνας 1 ενεργοποιείται με βαθμό 0.12
Ο κανόνας 2 ενεργοποιείται με βαθμό 0.9
.
.
Ο κανόνας n ενεργοποιείται με βαθμό 0.05
Εδώ φαίνεται πως η δεδομένη είσοδος ταιριάζει πιο πολύ με το δεύτερο κανόνα ελέγχου. Τέλος, ένα πολύ βασικό χαρακτηριστικό που προκύπτει εδώ είναι το γεγονός ότι με αυτό τον τρόπο μπορεί να παραχθεί έλεγχος ακόμα και για περιπτώσεις που δεν έχουν συμπεριληφθεί στους κανόνες. Έτσι, βλέπουμε συχνά πολύπλοκα συστήματα να ελέγχονται από σχετικά μικρό αριθμό κανόνων.
3. Ο προσαρμοστής εξόδου. Η μονάδα αυτή είναι απαραίτητη για την οδήγηση του συστήματος που πρόκειται να ελεγχθεί. Όπως αναφέραμε και προηγουμένως, η έξοδος του ασαφούς ελεγκτή είναι ένα ασαφές σύνολο και πρέπει να μετατραπεί σε μια πραγματική τιμή. Η μετατροπή αυτή γίνεται συνήθως με τρεις τρόπους:
α) Η μέθοδος του μέσου όρου των μεγίστων. Σύμφωνα με αυτή βρίσκουμε τις τιμές ελέγχου για τις οποίες η συνάρτηση ομάδας του συνόλου ελέγχου είναι μέγιστη, και από αυτές τις τιμές υπολογίζουμε το μέσο όρο. Η μέθοδος αυτή λαμβάνει υπ` όψιν της τους ελέγχους με το μεγαλύτερο επίπεδο ενεργοποίησης αλλά χάνει πληροφορία για τις υπόλοιπες τιμές καθώς και για τη μορφή της συνάρτησης ομάδας του συνόλου ελέγχου.
β) Η μέθοδος του κέντρου βαρύτητας. Εδώ υπολογίζεται το κέντρο βάρους (η μέση τιμή) του συνόλου ελέγχου. Εφαρμόζοντας αυτή τη μέθοδο πετυχαίνουμε ομαλές μεταβάσεις και η πληροφορία για τη μορφή της συνάρτησης ελέγχου λαμβάνεται υπ` όψιν στην όλη διαδικασία.
γ) Η τροποποιημένη μέθοδος του κέντρου βαρύτητας. Εδώ γίνεται μια πιο πλήρης επεξεργασία των αποτελεσμάτων του ασαφούς ελεγκτή. Γνωρίζοντας τα κέντρα βαρύτητας όλων των συναρτήσεων ελέγχου των κανόνων του συστήματος, ui, και τα επίπεδα ενεργοποίησης του κάθε ελέγχου, λi, υπολογίζεται η έξοδος από τη σχέση
u=Σiλiui/Σiλi
Και τις τρεις παραπάνω μεθόδους τις συναντούμε πολύ συχνά σε διάφορες εφαρμογές. Η μεγαλύτερη εκμετάλλευση πληροφορίας γίνεται από την τροποποιημένη μέθοδο του κέντρου βαρύτητας, η οποία δίνει τη μεγαλύτερη εξάρτηση της εξόδου από τους κανόνες του συστήματος.
Στο σχήμα που ακολουθεί φαίνεται η έξοδος ενός ασαφούς ελεγκτή με τρεις κανόνες.
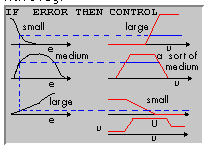
Εκείνο που πρέπει να προσέξει κανείς στο παραπάνω σχήμα είναι ο τρόπος με τον οποίο ενεργοποιείται ο κάθε κανόνας και πως όλοι οι κανόνες συμβάλλουν για τη δημιουργία της εξόδου.

Δείτε επίσης: